AVL Tree & B-Tree

Muhammad Raul Taqi Athallah // 2301893013

AVL Tree & B-Tree

• AVL Tree

AVL Tree adalah Binary Search Tree yang memiliki perbedaan tinggi/level maksimal 1 antara subtree kiri dan kanan. AVL Tree digunakan untuk menyeimbangkan Binary Search, mempersingkat waktu pencarian, dan menyederhanakan bentuk tree.

Cara menentukan Height :

• Jika root tidak memiliki subtree, height = 0.
• Jika node adalah leaf, height = 1.
• Jika internal node, maka height = height tertinggi dari anak + 1.

Cara menentukan Balance Factor :

• Selisih height antara anak kiri dan kanan, jika tidak memiliki anak, dianggap

AVL Tree Operations :

1. Insertion

2. Deletion

Insertion

Ada 4 Kondisi yang biasa terjadi saat Insertion dilakukan, yaitu :

1. Node terdalam terletak pada subtree kiri dari anak kiri T (left - left)
2. Node terdalam terletak pada subtree kanan dari anak kanan T (right - right)
3. Node terdalam terletak pada subtree kanan dari anak kiri T (right - left)
4. Node terdalam terletak pada subtree kiri dari anak kanan T (left - right)

Empat kondisi diatas bisa diatasi dengan melakukan rotasi. Kondisi 1 & 2 dengan single rotation, dan Kondisi 3 & 4 dengan double rotation.

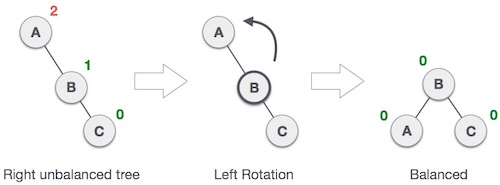
1. Left Rotation, disaat node diinsert ke subtree kanan dari subtree kanan.

Caranya adalah merubah A menjadi subtree kiri dari B, B menjadi root.

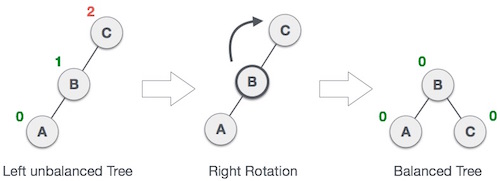
2. Right Rotation, disaat node diinsert ke subtree kiri dari subtree kiri.

Caranya adalah merubah C menjadi subtree kanan dari B, B menjadi root.

3. Left-Right Rotation, rotasi gabungan dari Left rotation yang diikuti dengan Right rotation.

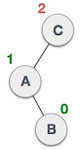Node diinsert ke subtree kanan dari subtree kiri yang membuat C menjadi unbalanced node. kasus ini membuat left-right rotation dilakukan.

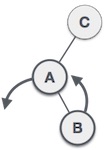Pertama, kita melakukan left rotation di subtree kiri dari C, yang menjadikan A subtree kiri dari B.

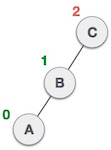Setelah tree menjadi seperti yang tergambarkan diatas, selanjutnya lakukan Right rotation, dan tree akan balanced.

4. Right-Left Rotation, rotasi gabungan dari Right rotation yang diikuti dengan Left rotation.

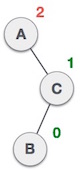Node diinsert ke subtree kiri dari subtree kanan, yang menjadikan node A unbalanced dengan balance factornya adalah 2.

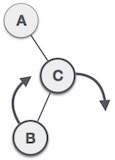Pertama, lakukan right rotation C node, yang menjadikan C menjadi subtree kanan dari B, B menjadi subtree kanan dari A.

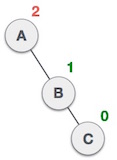Setelah seperti ini, lakukan left rotation dan tree akan balanced.

Deletion

Operasi Deletion node pada AVL Tree sama seperti pada Binary Search Tree. Node yang dihapus digantikan oleh node terbesar pada subtree kiri atau node terkecil pada subtree kanan.

Ada 2 Kasus yang biasanya terjadi saat operasi delete dilakukan, yaitu :

• Jika node yang akan dihapus berada pada posisi leaf/node tanpa anak, maka bisa langsung dihapus
• Jika node yang akan dihapus memiliki anak, maka proses penghapusan harus di cek kembali untuk menyeimbangkan Binary Search Tree.
• Anggap T adalah node yang harus diseimbangkan kembali :
• Kasus 1 : node terdalam terletak pada subtree kiri dari anak kiri T (left-left)
• Kasus 2 : node terdalam terletak pada subtree kanan dari anak kanan T (right-right)
• Kasus 3 : node terdalam terletak pada subtree kanan dari anak kiri T (right-left)
• Kasus 4 : node terdalam terletak pada subtree kiri dari anak kanan T (left-right)

• B-Tree

B-Tree adalah sebuah m-ary balanced search tree khusus yang digunakan dalam basis data karena strukturnya memungkinkan data yang disimpan untuk disisipi, dihapus, dan diambil dengan jaminan proses dengan waktu terburuk, di mana simpulnya terdiri dari (m/2) sampai m buah simpul anak, di mana m > 1 merupakan bilangan bulat. m adalah orde. Akar pohon B-Tree paling sedikit memiliki 2 simpul anak. Ini adalah struktur yang baik jika pohon digunakan pada memori yang lambat, karena ketinggian dan jumlah akses dapat diperkecil dengan mengambil bilangan m yang besar. Balanced Tree atau pohon seimbang adalah pohon di mana tidak ada simpul daun yang lebih panjang terhadap daun yang lain.

Insert

Steps :

1. Cari dulu dimana key untuk lokasi peletakan node di sebuah tree
2. Jika di leaf yang hanya terisi 2-node maka kita bisa langsung insert
3. Jika leaf sudah 3-node dorong data tengah antara A, B dan  kunci (A dan B adalah dua data dalam bahwa 3-node) ke parentnya dan membagi dua data yang tersisa menjadi dua 2-simpul. Rekursif sampai  parent tidak memiliki jumlah node yang lebih dari 2. 

Delete

Steps :

1. Pilih node yang ingin kita hapus
2. Jika leaf sudah 3-node, kita tinggal hapus node dan menjadi leaf yang berisi 2-node.
3. Jika berada di 2-node:
1. Jika parent adalah 3-node, mendapatkan satu nilai dari itu. Jika child yang satu level adalah 3-simpul, dorong satu nilai dari child ke parent  (untuk membuat parent 3-simpul lagi). Jika child yang selevel adalah 2-node, membuat parent 2-node dan menggabungkan node saat ini dengan child yang selevel.
2. Jika induk 2-node. Jika saudara kandung adalah 3-node kemudian mendapatkan satu nilai dari parent dan mendorong satu nilai dari child ke parent nya. Lain menggabungkan parent dengan child yang selevel.
4. Rekursif sampai  parent tidak memiliki jumlah node yang lebih dari 2.